Building Blocks

The basic building blocks of PGL are very simple consisting of a few curve types and a surface mesh class using the so-called Coons surface to construct a surface based on four connected curves.

Curves

Curve

The basic class for all curves is the PGL.main.curve.Curve class, and can operate on both 2D and 3D curves. The class computes the running length of the curve, direction vectors along the curve, and allows you to redistribute the curve. Other methods relate to rotation and translation of the curve, splitting and joining with other curves.

import numpy as np
from PGL.main.curve import Curve

# create the points on the curve:
sin = np.sin(np.linspace(0, np.pi*2, 20))
points = np.array([np.linspace(0, np.pi*2,20), np.zeros(20), sin]).T
l = Curve(points=points)

Line

The PGL.main.curve.Line class inherits from PGL.main.curve.Curve adding a convenience method for generating a line.

SegmentedCurve

The PGL.main.curve.SegmentedCurve class inherits from PGL.main.curve.Curve, enxtending it with methods to add individual segments.

BezierCurve

The PGL.main.bezier.BezierCurve class inherits from PGL.main.curve.Curve, adding methods for constructing a Bezier curve based on a list of control points:

import numpy as np

from PGL.main.bezier import BezierCurve

# create the points on the curve:
c = BezierCurve()
c.ni = 21
c.add_control_point(np.array([0, 0, 0]))
c.add_control_point(np.array([0, 0.2, 0]))
c.add_control_point(np.array([0.2, 0.2, 0]))
c.add_control_point(np.array([0.5, 0.2, 0]))
c.add_control_point(np.array([1., 0.005, 0]))
c.update()

AirfoilShape

The PGL.components.airfoil.AirfoilShape class extends the PGL.main.curve.Curve class with airfoil geometry specific methods. The class extends the Curve.redistribute method with airfoil specific distribution of points, closing and opening of the trailing edge. A simple example of how to redistribute the points on an airfoil and close its trailing edge is shown below:

import numpy as np
from PGL.components.airfoil import AirfoilShape

c = AirfoilShape(points=np.loadtxt('data/ffaw3241.dat'))
c.redistribute(ni=257, close_te=11)

BezierAirfoilShape

The PGL.components.airfoil.BezierAirfoilShape is a wrapper around the PGL.components.airfoil.AirfoilShape class which fits Bezier curves to an airfoil shape and subsequently allows manipulation of its shape via the Bezier control points.

In the example below we fit Bezier curves to the FFA-W3-301 airfoil:

import numpy as np
import matplotlib.pylab as plt

from PGL.components.airfoil import BezierAirfoilShape
from PGL.components.airfoil import AirfoilShape

b=BezierAirfoilShape()
b.afIn = AirfoilShape(points=np.loadtxt('data/ffaw3301.dat'))
b.spline_CPs = np.array([0, 0., 0.1, 0.2, 0.4, 0.7,1])
# b.fix_x = False
b.fit()

plt.plot(b.afIn.points[:,0], b.afIn.points[:,1], label='org')
plt.plot(b.afOut.points[:,0], b.afOut.points[:,1], label='fitted')
plt.plot(b.CPl[:,0], b.CPl[:,1], 'r--o', label='Lower surface CPs')
plt.plot(b.CPu[:,0], b.CPu[:,1], 'r--o', label='Upper surface CPs')
plt.axis('equal')
plt.legend(loc='best')
plt.show()

The resulting fitted airfoil and Bezier control points are shown below:

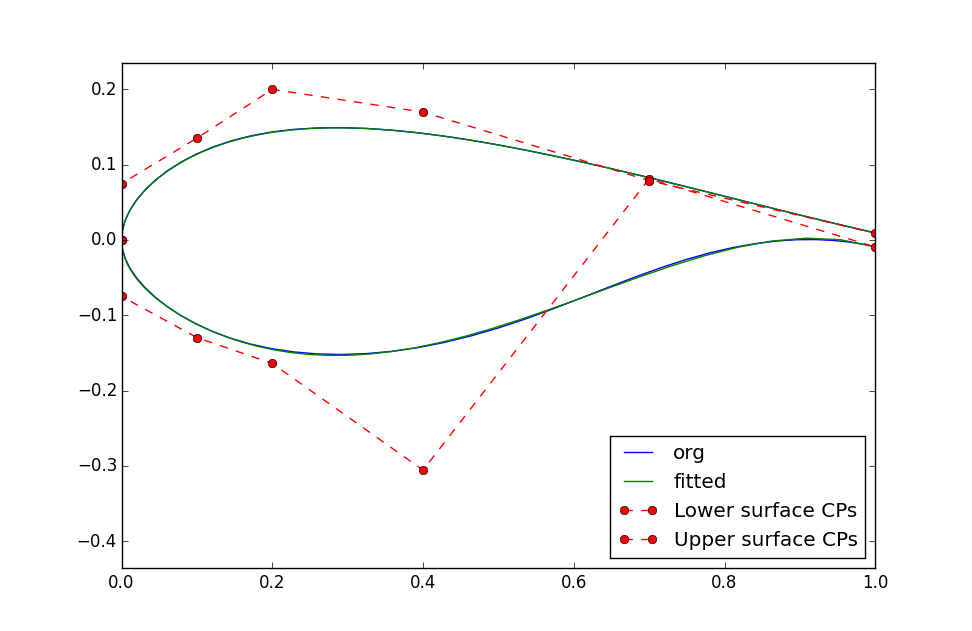
BlendAirfoilShapes

The PGL.components.airfoil.BlendAirfoilShapes class generates interpolated airfoil shapes based on a user defined airfoil family. The blended airfoil shape is interpolated using a cubic interpolator.

import numpy as np

from PGL.components.airfoil import BlendAirfoilShapes

# make an airfoil interpolator to reproduce the DTU 10MW RWT
interpolator = BlendAirfoilShapes()
interpolator.ni = 257
interpolator.spline = 'pchip'
interpolator.blend_var = [0.241, 0.301, 0.36, 1.0]
for f in ['data/ffaw3241.dat',
          'data/ffaw3301.dat',
          'data/ffaw3360.dat',
          'data/cylinder.dat']:

    interpolator.airfoil_list.append(np.loadtxt(f))
interpolator.initialize()

# interpolate a 25% airfoil
af = interpolator(0.25)

Surface Generation

Coons Patch

To generate smooth surfaces PGL uses Coons patches, PGL.main.coons.CoonsPatch, which are constructed from four edges and linearly or cubicly interpolated to form a surface.

# create the edges
sin = np.sin(np.linspace(0, np.pi*2, 20))
l0 = Curve(points=np.array([np.zeros(20),        np.linspace(0, 2*np.pi,20), np.zeros(20)]).T)
l1 = Curve(points=np.array([np.ones(20)*np.pi*2, np.linspace(0, 2*np.pi,20), sin]).T)
l2 = Curve(points=np.array([np.linspace(0, np.pi*2,20), np.zeros(20),      sin]).T)
l3 = Curve(points=np.array([np.linspace(0, np.pi*2,20), 2*np.pi*np.ones(20), sin]).T)

# create an instance of the CoonsPatch class
c = CoonsPatch(20, 20)

c.add_edge(0, l0.points)
c.add_edge(1, l1.points)
c.add_edge(2, l2.points)
c.add_edge(3, l3.points)
c.update()

The PGL.main.coons.CoonsPatch class generates as output a Block instance, which has a plot method that uses Mayavi. If you have Mayavi installed you can plot the surface, showing the four edges:

c.P.plot_surface_grid(edges=True)
# plot the surface normal of the patch
c.P.plot_normals()

You should get something like this:

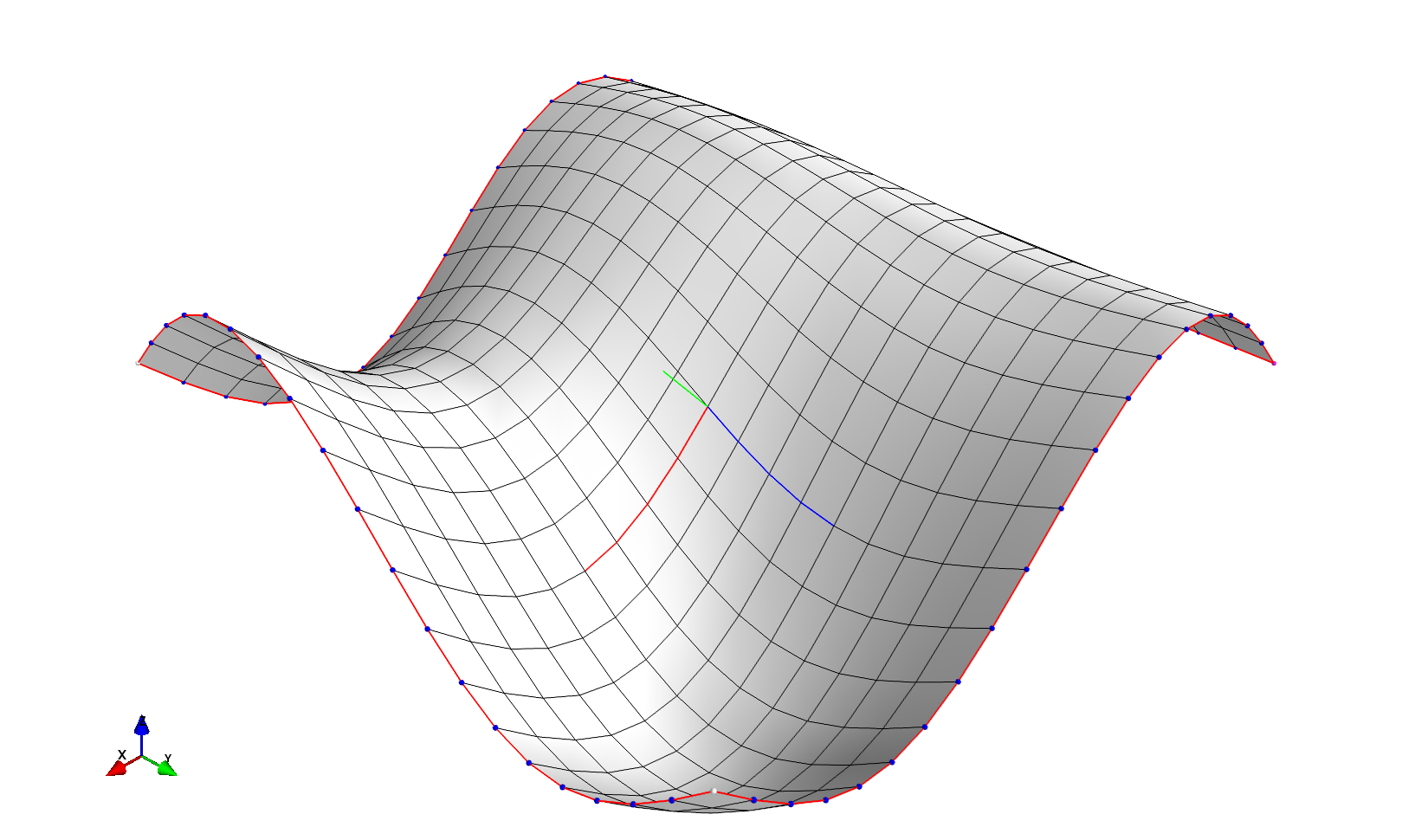
For this plot we chose to use a cubic interpolant, but in some cases a linear interpolant can be better suited, when for example a cubic surfaces creates too large overshoots. To make a Coons surface with a linear interpolant, simple instantiate the CoonsPatch class with interpolant='linear'.

The combination of Bezier curves and Coons patches makes for a very versatile tool for generating parametric surfaces.

As shown in the below example we can quite effortlessly create a smooth blend of two airfoil shapes forming a winglet shape.

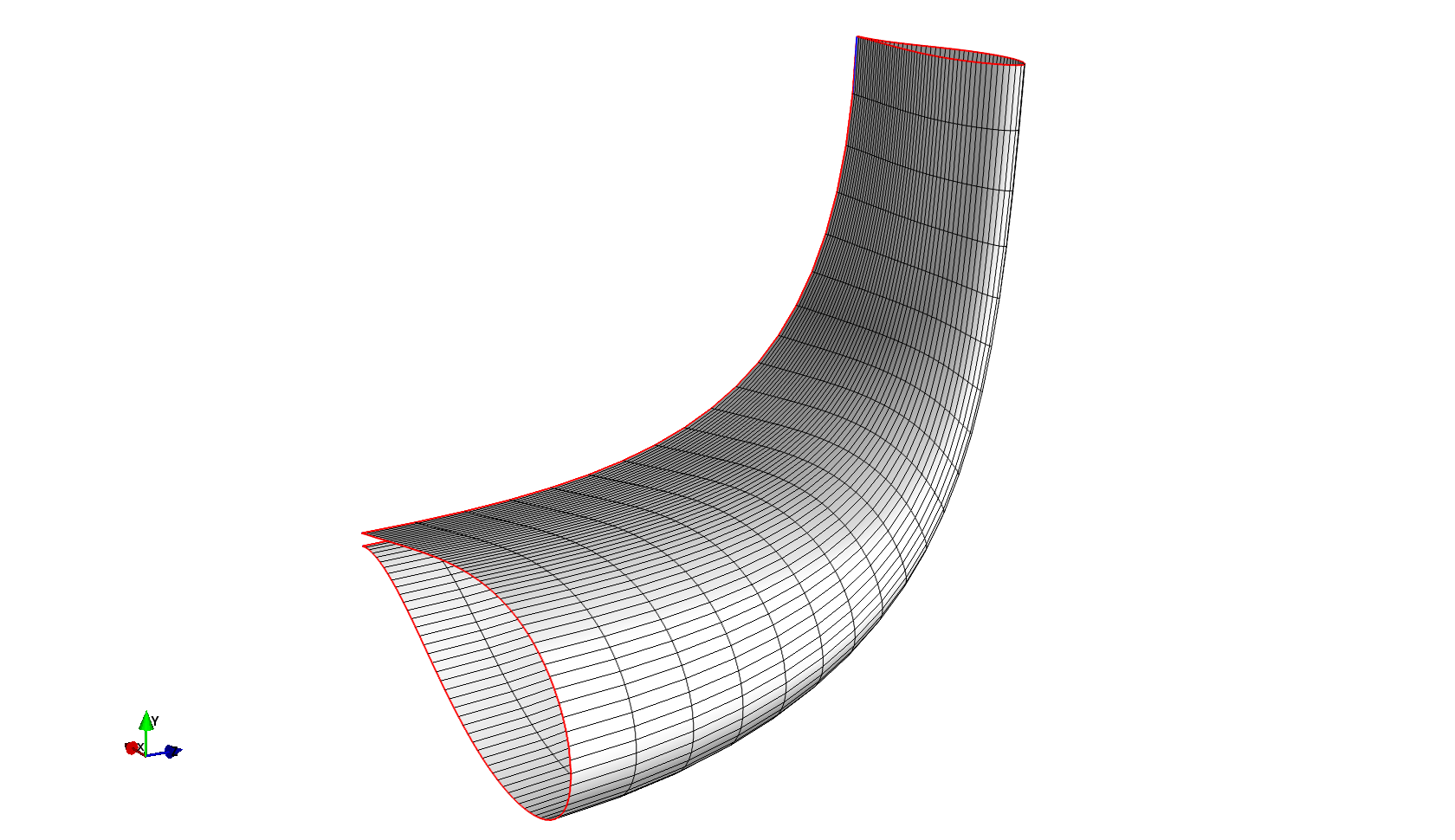
ExtrudedSection

The PGL.main.extruded_section.ExtrudedSection class can be used to generate extruded surfaces from two cross-sectional shapes. The two cross-sections can be oriented arbitrarily in space, and will be connected by Bezier curves for which it is possible to control the ends of the curves. The below code can be found in PGL/examples/coons_extrusion.py.

import numpy as np

from PGL.main.coons_extrusion import CoonsExtrusion
from PGL.main.airfoil import AirfoilShape

l0 = AirfoilShape(points=np.loadtxt('data/ffaw3241.dat'), nd=3)
# l0.spline_CPs = np.array([0, 0., 0.1, 0.2, 0.4, 0.7,1])
# l0.fit()
l0.redistribute(ni=129, dLE=True, dTE=0.001)
l0.translate_z(-1)

l1 = AirfoilShape(points=np.loadtxt('data/ffaw3241.dat'), nd=3)
# l0.spline_CPs = np.array([0, 0., 0.1, 0.2, 0.4, 0.7,1])
# l0.fit()
l1.redistribute(ni=129, dLE=True, dTE=0.001)

l2 = AirfoilShape(points=np.loadtxt('data/ffaw3241.dat')*12./24., nd=3)
l2.redistribute(ni=129, dLE=True, dTE=0.001)
l2.scale(0.6)
l2.rotate_x(-90.)
l2.translate_x(1.25)
l2.translate_z(1)
l2.translate_y(1.5)


d0 = CoonsExtrusion(l0.points, l1.points)
d0.np = 2
# th
d0.fW0 = 0.25
d0.fW1 = 0.25
d0.interpolant='linear'
d0.create_section()
d0.setZero(0, 'z')
d0.setZero(1, -1)
d0.update_patches()

d1 = CoonsExtrusion(l1.points, l2.points)
d1.np = 1
# th
d1.fW0 = .8
d1.fW1 = 0.5
# d.interpolant='linear'
d1.create_section()
d1.setZero(0, 'z')
#  d1.setZero(1, np.array([-.45, -.9, -.125]))
d1.update_patches()

In the code snippet we construct two sections, one a simple section from a blend of two airfoils, and the other slightly more complex, where the second cross-section is rotated and translated to form a winglet like surface.

If you run it, you should get something like this:

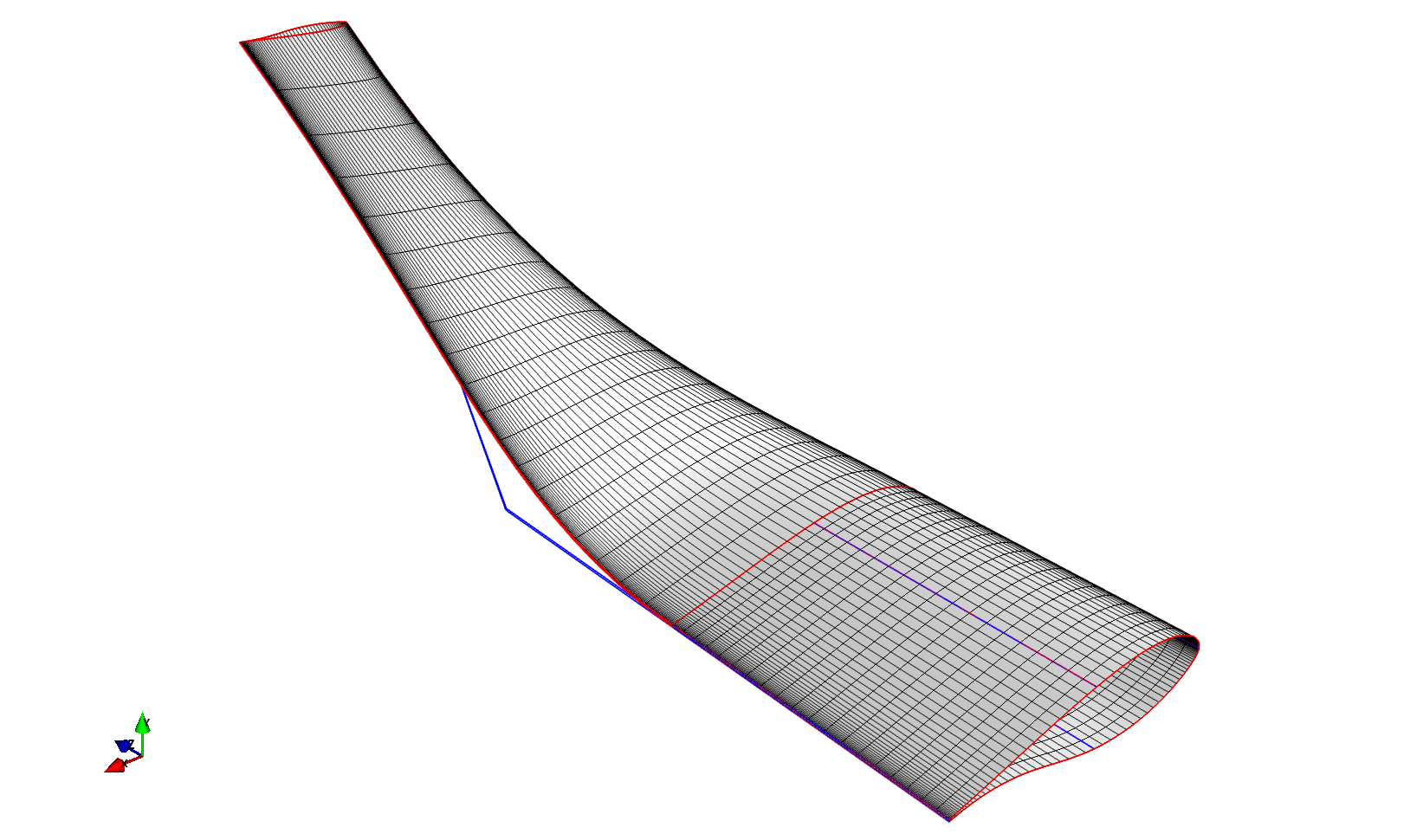
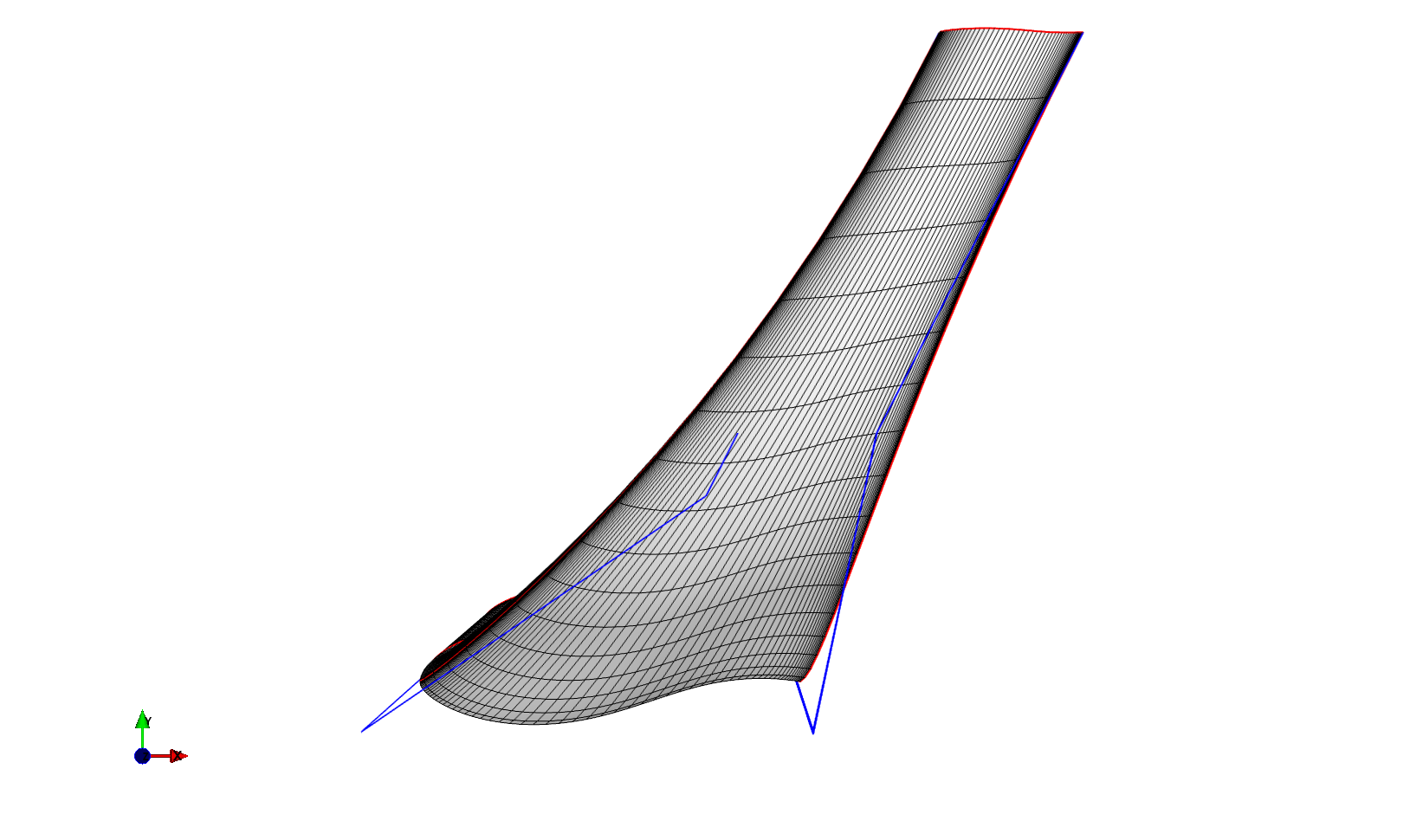
As you can see in the figure the blue curves show the location of the control points of the edges of the surface patches. The default behaviour is to connect the two sections with straight lines, however, in this example we want to generate a winglet shape, so we don’t want the edges to be straight lines. In the code we call the setZero function, which allows us to enforce the gradient of the edge curves at their end points. At the first section we want the curve to shoot in the positive z-direction, whereas at the second section we want it to shoot in the negative y direction. However, instead of specifying ‘y’, we instead provide the method with a directon vector which allows us to give the winglet a bit of sweep and cant.

While the above example can be used to generate winglets, there are a few parameters we’d like more control over when making winglets, so for this purpose use the WingletTip class.

BezierPatch

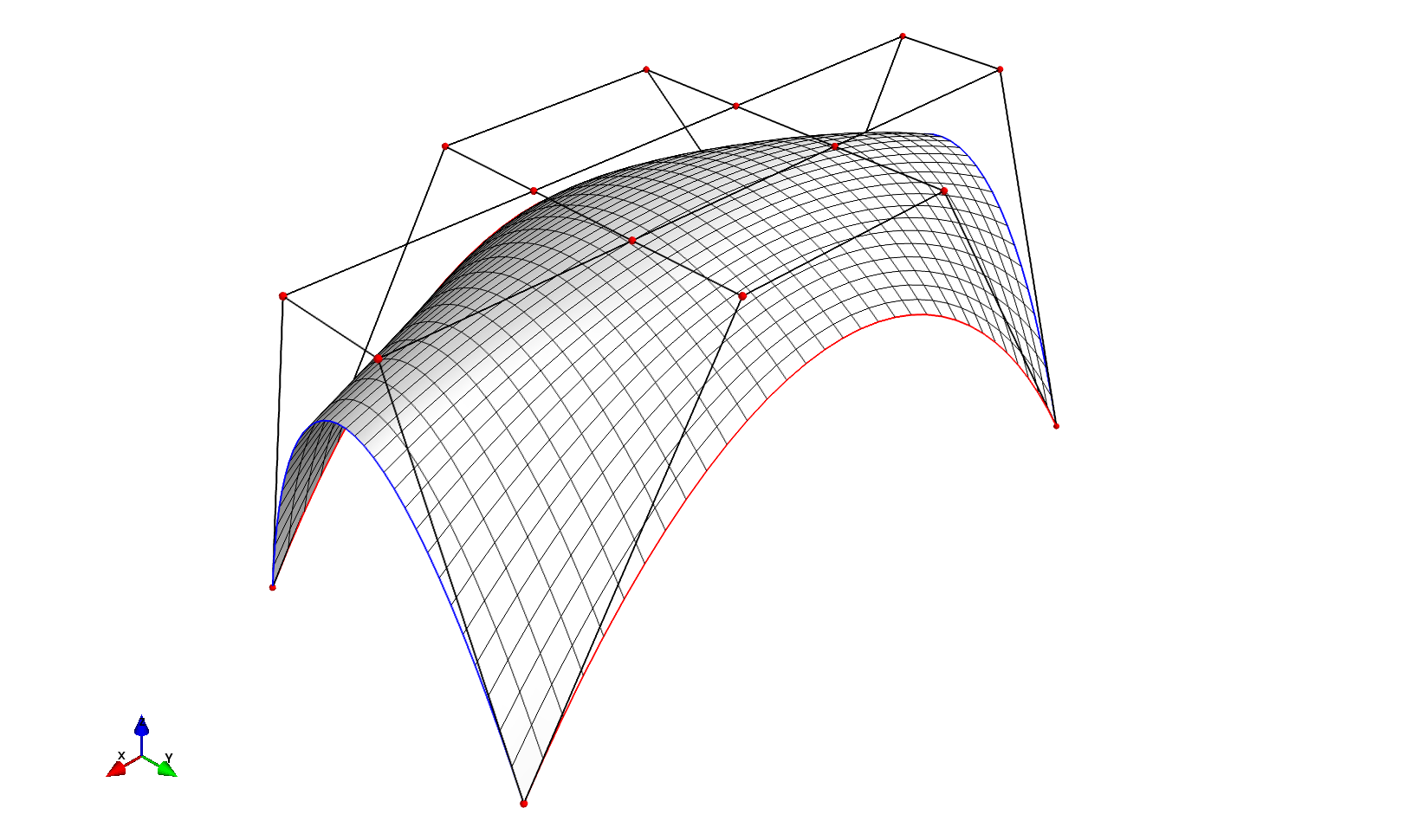
An alternative to the PGL.main.coons.CoonsPatch is the PGL.main.bezierpatch.BezierPatch class which generates a smooth surface based on a grid of control points.

A simple example of how to use this class is shown below, generated by a grid of control points (m, n) = (4, 4), ranging from 0 < x < 2 and 0 < y < 1 and z = 1., except at the four corners where z = 0.:

import numpy as np
from PGL.main.bezierpatch import BezierPatch


p = BezierPatch()
m = np.meshgrid(np.linspace(0, 2, 4), np.linspace(0, 1, 4))
p.CPs = np.ones((4, 4, 3))
p.CPs[:, :, 0] = m[0]
p.CPs[:, :, 1] = m[1]

# zero at corners
p.CPs[0, 0, 2] = 0.
p.CPs[-1, 0, 2] = 0.
p.CPs[0, -1, 2] = 0.
p.CPs[-1, -1, 2] = 0.

p.update()

p.P.plot_surface_grid(edges=True)
p.plot_CPs()

which should generate a surface as shown below: